tiny diffrast notes

the forward rendering process as a function : $f: x \rightarrow y$

• x: scene parameters
• y: image data
  inverse process : $f^{-1}: y \rightarrow x$

even when provided with $y$ and $f$, computing $f^{-1}$ and $x$ is not at all straightforward. What we can often do, however, is compute the derivative $$ \frac{\partial f}{\partial x}$$This derivative is useful because

• gradually update scene parameters $x$
• make the image data produced by $f(x)$ gradually more similar to some ground truth image data.

In this project:
explore, explain and implement two different state-of-the-art inverse rendering approaches that rely on triangle rasterization: Nvdiffrast (NVDR) and Rasterize-Then-Splat (RTS)

ML framework cannot simply implement differentiable rasterization.

• the algorithm is static.(known at compile time)
• Tensor-heavy and Control-light
• But for rasterization -> small-data and Control-heavy
• Triangles are processed parallel, and how each triangle is processed depends on the value of the triangle vertices, which are not known at the compile time. BVH, triangle索引关系都不是tensor
• So rasterization algorithm requires fine control flow within a parallel computing framework

Frameworks that meet requirements:

• Dr. Jit was developed specifically for the application of differentiable ray tracing.
• Slang : support for automatic differentiation, targeting inverse rendering applications.
  (SlangD paper Appendix C includes an excellent discussion of the design space of automatic differentiation frameworks. Additionally, Christopher Rackauckas has written a few good blog posts (1, 2) on the topic.)

Taichi

• embedded within Python and is easy to read and write.
• supports both CUDA and CPU backends.
• Warp framework is extremely similar to Taichi and may even be more advanced at the time of writing this.
• supports automatic differentiation.
• follows a single instruction multiple data (SIMD) programming model, similar to Slang.
  • SIMD: 一条指令控制多个数据并行计算，并行计算模型，特别在GPU/shader语言中非常常见
  • 例如：

for (int i = 0; i < 4; ++i)
    a[i] = a[i] + 1;

在CPU上是顺序执行，但是在SIMD下，处理器可以“加 1”指令同时作用于 a[0], a[1], a[2], a[3]。

• Taichi has good support for advanced data structures.

• also has good support for real-time and interactive visualizations.

---

Learnable rotation

for Rotation

mathematical group

mathematical group: 所有的3D旋转组合的一个集合+操作规则，构成一个group
所有的3D旋转组成一个group，叫SO(3) (==要学==)

条件	意思
封闭性 closure	两个元素操作后结果还在这个集合里（比如两个旋转 compose 后还是旋转）
结合律 associativity	(a∗b)∗c=a∗(b∗c)(a * b) * c = a * (b * c)
单位元 identity	有个“不改变任何东西”的操作（比如恒等旋转）
逆元 inverse	每个操作都有“反操作”能还原（比如旋转 + 反方向旋转）

Differentiable manifold

manifold: 比如地球是一个球体，但放大到一个城市的大小，看起来又像是平的。局部是平的
SO(3) 这个群本身是一个 三维流形：它不是欧几里得空间，但在很小的局部能展开、做微分。

在欧几里得空间（比如 $\mathbb{R}^n$）中，对函数做微分，比如：

$$
f: \mathbb{R}^3 \rightarrow \mathbb{R}, \quad \frac{\partial f}{\partial x}
$$
这很自然：你把变量想象成“坐标”，沿着这些轴方向做导数就行了。

manifold虽然是“弯”的，但在每个点的局部，我们可以找一个tangent space，它是一个欧几里得空间！（相当于局部平面，在局部平面上做gradient，做优化，做梯度下降）

不能选的rotation representation:

• Euler angle一旦遇到gimbal lock后，就会信息丢失->旋转不可逆
• 对比Quaternion, SO(3)天生在manifold上，没有归一化问题。quaternion需要normalize

---

• CUDA: programmable components of GPU
• fixed-function resources: non-programmable components in GPU
  • 就是预制的功能，例如rasterizer固定算法不能改

模块	功能	说明
Vertex Assembler	组装顶点数据	从 buffer 中拉数据、送入 pipeline
Rasterizer	把三角形转成 fragment	固定算法，不能改
Depth Test	深度缓冲比较	固定规则，比较 z 值
Blending	颜色混合	alpha 混合规则写死
Texture Sampler	从纹理中采样	只支持规定的 filtering 模式（bilinear、mipmap）
现代 API（OpenGL / Vulkan / Metal）：

• shader → 是 programmable 的部分
• pipeline stage（raster / depth / blend）→ 是 fixed-function

deferred shading:
rasterization outputs image buffer that contain information related to triangle coverage and occlusion
G-buffers: contain geometry and texture information

Then the shading computation: use G-buffers to c ompute final color at each pixel.
So when implementing differentiable rasterizer, we must output buffers that provide sufficient information to support downstream shading operations.

differentiable rasterizerCommonly output 3 buffers:

• triangle id buffer : about which triangle is visible at each pixel in the image

• depth buffer

• barycentric coordinate buffer : must support gradient backpropagation

• multi-layer rasterization

• half-plane algorithm

  • core idea: triangle can be described by three edges
  • For each edge, define a linear function
  • based on the sign of the function, tells us which side of the edge a point is on.
  • for any point, we can evaluate three linear functions to determine if the point is inside or outside of a triangle.
  • compute barycentric coordinates.

测试：P 是否在 AB 的左侧
测试：P 是否在 BC 的左侧
测试：P 是否在 CA 的左侧

判断使用 cross product

设一条边为 $\vec{e} = B - A$，点 $P$ 的向量为 $\vec{v} = P - A$，那么：
$$
\text{cross}(\vec{e}, \vec{v}) = (B - A) \times (P - A)
$$

• 如果结果 > 0，表示 $P$ 在 AB 的左侧
• 如果 < 0，则在右侧
• 如果 = 0，点在边上

GPU parallel rasterizer

CTA：
Cooperative Thread Array, 是cuda中的术语，代表一组可以协同工作的thread block。每个CTA包含多个THREAD，可以共享资源并同步工作

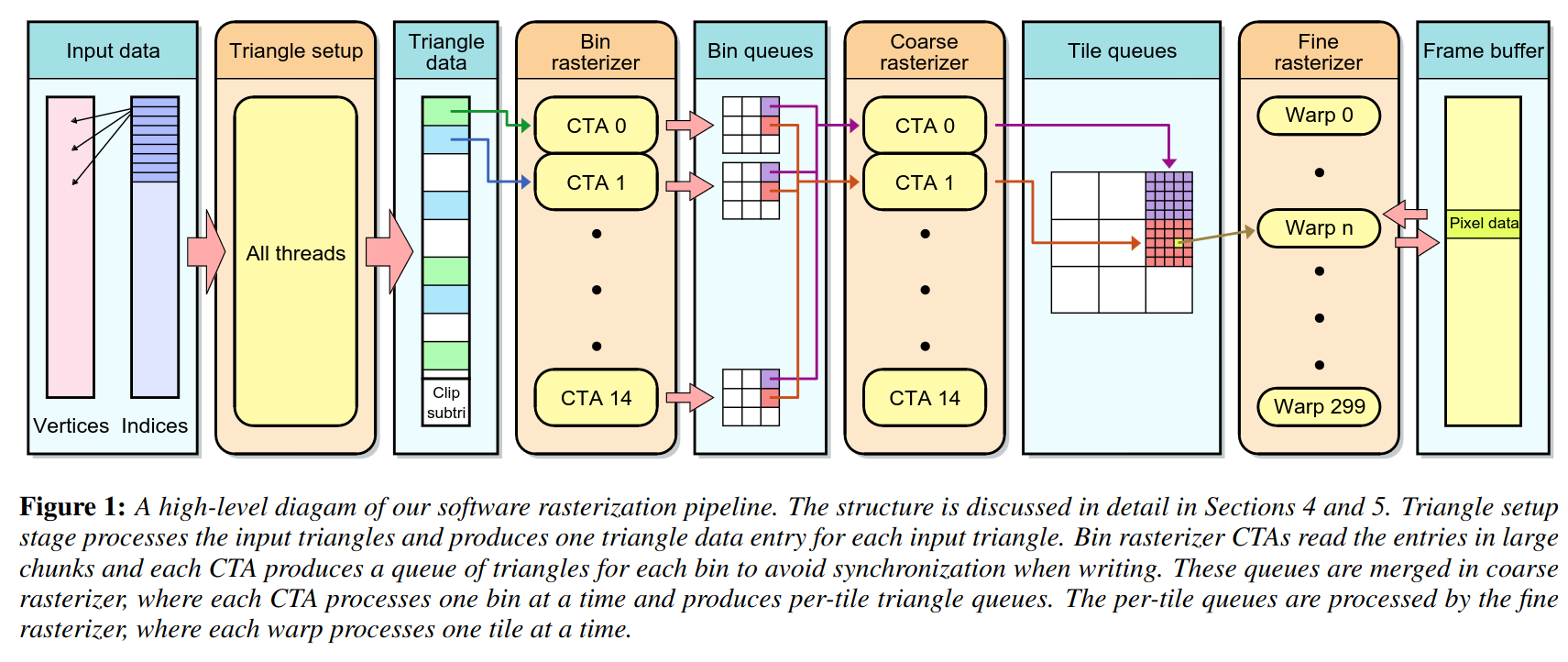
在GPU上可并行的rasterization:

1. Input data 输入数据阶段：包括顶点（Vertices）和索引（Indices）。
2. Triangle setup 三角形设置阶段：处理输入的三角形，并生成每个三角形的数据条目。all triangles are processed in parallel.
   • output: is a data structure containing all triangle information that is required for future
   • need: edge functions (whether pixel inside a triangle), depth parameters (Z-buffer)

bin and coarse rasterization stage:
Goal: prepare triangle processing queues for each 8x8 pixel tile in the image
3. Bin rasterizer 分块光栅化阶段：多个CTA（并行计算单元，下面解释）读取大量三角形数据，输出分块三角形队列。A triangle is added to a tile queue if it overlaps part of the tile.
4. Bin queues 分块队列阶段：存储分块后的三角形队列。
5. Coarse rasterizer 粗光栅化阶段：每个CTA处理一个分块，生成每个瓦片的三角形队列。
6. Tile queues 瓦片队列阶段：存储每个瓦片的三角形队列。

7. Fine rasterizer 细光栅化阶段：每个warp（线程组）处理一个瓦片，最终输出像素数据。
   • use triangle edge functions to determine if a pixel is within a triangle.
   • also do z-buffer. if a pixel inside a triangle, the depth at the pixel is evaluated and checked against the depth buffer to see if the triangle is occluded at that pixel. 针对每个像素都会计算depth value，然后和这个tile里面的其他的做对比
   • each tile is processed in parallel
   • in each tile, the triangle in the tile queue are processed sequentially
     • because z-buffer need information about previously processed triangles.
8. Frame buffer 帧缓冲区：存储生成的像素数据。

4 stages

notes:
in the tiny diffrast practice, we dont do bin and coarse rasterization stages.
4 stages (4 separate taichi kernels)

1. vertex_setup : all vertices are processed in parallel
   • transform vertices from world space to clip space
   • kernel is differentiable and will do backward pass
   • backprop gradients from clip vertices -> camera matrices and mesh vertices
2. triangle_setup: all triangles are processed in parallel
   • add processed triangles into tile queues in preparation for the next stage
   • this kernel is not differentiable not involved in backward pass
3. rasterize: each tile is processed in parallel
   • compute pixel coverage for each triangle
   • also performing z-buffer
   • this kernel is not differentiable and not in backward pass
   • triangles are taken from the rasterization queue and processed sequentially
4. compute_barycentric: each pixel is processed in parallel
   • kernel compute the barycentric coordinates for each pixel
   • this kernel is differentiable and will do backward pass
   • backprop gradient from barycentric image buffer -> the clip vertices intermediate data field

triangle edge function: check if the pixel is within the triangle

• if the pixel inside the triangle, the pixel depth also evaluated and check against depth buffer, to check if the triangle should appear in the first layer, or the second layer, or no layer of the image buffer.
• if triangle does appear in one of layer, values are written to the appropriate pixels in the triangle id and depth buffers

划分tile

# layout pixel fields with tile/pixel/layer structure
# tiles -> 8x8 pixels  -> 2 layers
pixel_root = ( # 把整个root划分成二维网格，宽高分别是
  ti.root.dense(ti.ij, (self.n_x_tiles , self.n_y_tiles))
  .dense(ti.ij, (8 ,8 ))
  .dense(ti.k, 2)
)

划分bin

bin并不是在field表示出来的，他是逻辑上的分区，用来激素triangle enqueue时的遍历判断(coarse culling)。 所以bin是在enqueue_triangle(…)函数里面，纯计算时动态构造的AABB，没有任何field对应

1. bin 粗判断：快速跳过和三角形 AABB 不相交的大区域；
2. tile 精判断：bin 里再细分 tile，做精确交叉判断并 append；

clip vertices 是世界空间 -> 相机空间（view） -> 投影空间（projection）后还没有除以w的那个

SetupTriangle

为每个三角形构建好「屏幕包围盒 + 边缘函数 + 深度插值」这三个 rasterizer 最核心的计算结构。
☑️ 功能流程

• 做 perspective divide：从 clip space 得到 ndc
• ndc -> screen：得到像素空间下的位置
• 为避免整数溢出，做了 screen_origin 偏移
• 乘 subpixel_factor 做高精度光栅
• 计算三角形面积，cull 背面和退化三角形
• 用整数做 edge function 的 step vector 和 origin bias
• 构造 edge function：A_x + B_y + C
• 计算 depth 插值参数（其实是线性函数）

最后设置一个标志 enqueue = True，表示这个三角形可以参与光栅化。